Calculation bimetallic actuator
How much does a bimetal actuator bends at a certain temperature and how is this calculated?
Sketch of a deflected bimetallic actuator
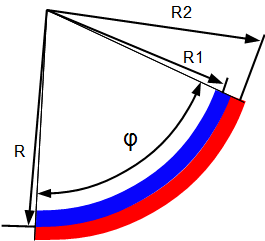
A bimetallic element is composed of two materials which are joined together and expand differently with changes in temperature. If the material 2 (shown in red) expands more than when heated material 1 (shown in blue), the material composite curves. The radius of curvature and thus the deflection at the end can be calculated.
Material 1 is blue Material 2 is red. The materials are firmly bonded together.
R: neutral fiber of the bimetallic actuator
R1: neutral fiber of the material 1
R2: neutral fiber of the material 2
f: Included angle in radians
A: Coefficient of Thermal Expansion
delta T: temperature difference for hibernation (bimetallic actuator straight)
l0: Length of the bimetallic actuator in the straight state
The length of a metal at a given temperature is:
Furthermore, the following applies:
Change in length of the materials to each other:
Change in length due to the geometry:
Equating the two above formulas gives:
After canceling:
Since bimetallic actuators are usually constructed from two materials with the same thickness d remains valid:
it follows:
Changing according to R.
The formula for the bimetallic actuator:
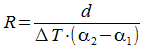
Note: This is the minimum bending radius, since the modulus of elasticity of the materials was not taken into account. In reality, the radius of which is slightly larger.
Example iron-nickel bimetallic actuator:
Talk to us
