Berechnung Bimetall Aktor mit Anleitung und Beispiel
Wie stark krümmt sich ein Bimetall Aktor bei einer bestimmten Temperatur und wie lässt sich das berechnen?
Skizze eines ausgelenkten Bimetall-Aktors
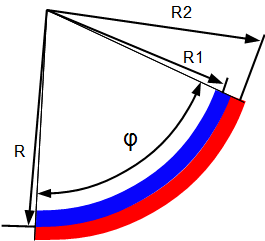
Ein Bimetall-Element besteht aus 2 Materialien, die miteinander verbunden sind und sich bei Temperaturänderungen unterschiedlich ausdehnen. Wenn sich das Material 2 (rot dargestellt) bei Erwärmung stärker ausdehnt als Material 1 (blau dargestellt), krümmt sich der Materialverbund. Der Krümmungsradius und damit die Auslenkung am Ende lässt sich berechnen.
Material 1 ist blau und Material 2 rot dargestellt. Die Materialien sind fest miteinander verbunden.
R: neutrale Faser des Bimetall-Aktors
R1: neutrale Faser des Materials 1
R2: neutrale Faser des Materials 2
φ: Eingeschlossener Winkel im Bogenmaß
α: Wärmeausdehnungskoeffizient
ΔT: Temperaturdifferenz zum Ruhezustand (Bimetall-Aktor gerade)
l0: Länge des Bimetall-Aktors im geraden Zustand
Die Länge eines Metalls bei einer gegebenen Temperatur ist:
Weiterhin gilt:
Längenänderung der Materialien zueinander:
Längenänderung aufgrund der Geometrie:
Gleichsetzen der zwei obigen Formeln ergibt:
Nach Kürzen:
Da Bimetall-Aktoren meist aus zwei Materialien mit gleicher Dicke d aufgebaut sind gilt weiter:
woraus folgt:
Umstellen nach R.
Die Formel für den Bimetall-Aktor:
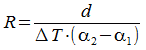
Hinweis: Dies ist der minimale Biegeradius, da der E-Modul der Materialien nicht berücksichtigt wurde. In der Realität ist der Radius geringfügig größer.
Beispiel Eisen-Nickel Bimetall-Aktor:
